2024年初中数学中考复习：三角形的五心

三角形的五心,是三角形的五个特殊点。

三角形的三条中线交于一点,该点称为三角形的重心;

三角形的三条高交于一点,该点称为三角形的垂心;

三角形的三条内角平分线交于一点,该点称为三角形的内心;

三角形各边上的垂直平分线交于一点,该点称为三角形的外心,等等。

这些点对三角形而言,都有若干重要的性质。

例如,内心就是三角形内切圆的圆心,外心就是三角形的外接圆的圆心。

三角形的五心，即外心、内心、重心、垂心、旁心,是“两考”(即中考与高考)和“两赛"(即初中数学竞赛与高中数学竞赛)中,经常出现的热点内容，也是初高中数学竞赛大纲中特别加强的内容。

与三角形五心有关的几何问题涉及知识广,难度大,技巧性强,方法灵活,是学生较难掌握的内容之一。

三角形外心的概念和性质

我们知道,经过线段中点且和这条线段垂直的直线,叫做这条线段的中垂线(或者称为垂直平分线).

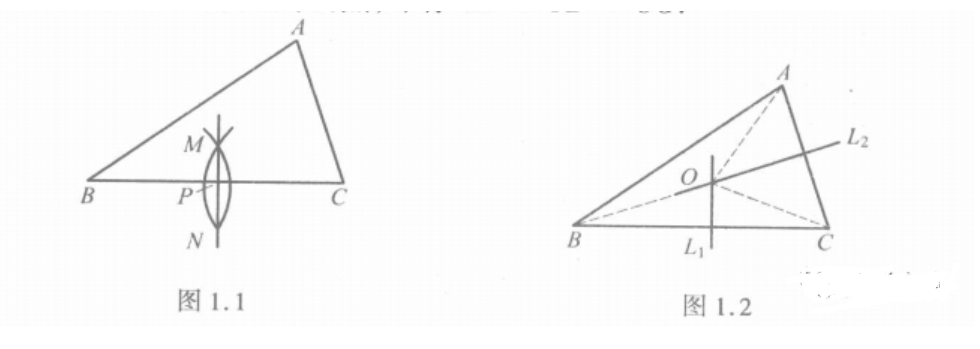
例如,图1.1中,直线MN就是线段BC的中垂线;或者说,它是△ABC的边BC的中垂线(即直线MN经过BC的中点P,而且垂直BC).

我们还知道,线段的中垂线上任何一点和这条线段的两个端点距离相等.

如图1.2中,0是线段BC的中垂线L上的点,则OB = OC. 由此可见,只要作出△ABC的边BC的中垂线L和边CA的中垂线L2,那么,L和L2相交的交点0就是和A,B, C距离相等的点,即有OA = OB = OC.

我们把三角形的三条高的交点H叫三角形的垂心,把这个定理叫三角形的垂心定理.

在证明过程中，我们的证明思路是:

先画一个新的三角形,把△ABC的三条高转化为这个新三角形的三条边的中垂线,而三角形的中垂线却是已知为共点的三条直线.这种证明方法也是证明三线共点的一种常用方法.

根据三角形的垂心定理易知如下一些基本性质:

(1)三角形的任何两条高线的交点, 就是三角形的垂心。

(2)三角形的两条高线相交于点H ,则第三个顶点与点H的连线垂直于第三边.

(3)若H是△ABC的垂心,则必有AH⊥BC,BH⊥CA,CH⊥AB.也就是说,在这样的四点A,B,C,H中,任何两点的连线必垂直于其余两点的连线.

(4)平面上的四点A,B,C,D中,若有一点是其余三点连线所构成的三角形的垂心，如D是△ABC的垂心，则这四点中任何一点都必定是其余三点连线所成的三角形的垂心,亦即为若D为△ABC的垂心，则A为△BCD的垂心，B为△CDA的垂心,C为△DAB的垂心.我们把这样的四点A,B,C, D称为一个垂心组.

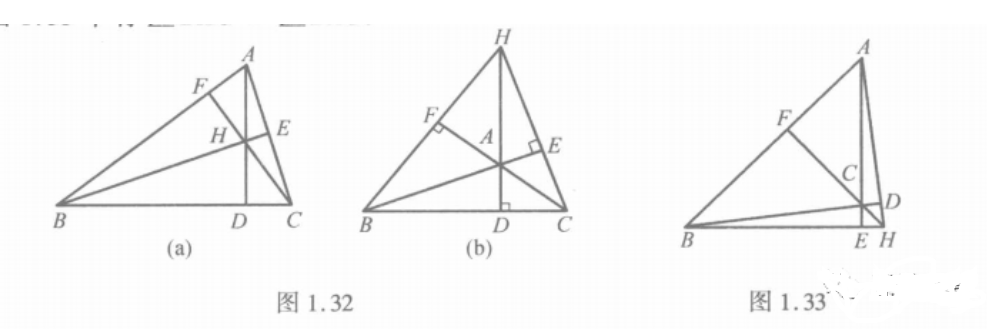
(5)若H为△ABC的垂心,则如图1.32中有∠BHC=180°-∠1BAC,如图1.33中有∠BHC=∠BAC.

三角形内心定理

三角形的三条内角平分线相交于-点,这个交点到三角形三边的距离相等.

我们把三角形三内角的交点，叫做三角形的内心.三角形的内心通常用大写英文字母“I”.很明显,任何三角形的三条内角平分线都在三角形内.

因此,三角形的内心位于三角形内.在图1.82中, OABC的三条内角平分线AD, BE, CF相交于一点1,且IQ = IR= IS,点“I”叫做三角形的内心.

在证明三角形内心定理的过程中,其思路与方法是证明三条直线中,其中两条直线的交点在第三条直线上,这也是证明三线共点的一种常用方法.

根据三角形内心定理,联想到三角形的外心、垂心和重心,不难知道:

(1)三角形的外心、垂心、重心和内心,一-般不在一条直线 上,更不会重合,只有当OABC为等腰(非等边,如AB = AC≠BC)时,其外心、垂心、重心和内心均在s ABC的底边BC的中线(此时中线、高及顶角的平分线三线合一)上，

当△ABC为正三角形时,外心、垂心、重心和内心重合为正三角形的中心.

反过来,这“四心”中任意两心重合,则这个三角形为正三角形.

(2)从三角形的一个顶点所作出的这个角的平分线和对边上的高、中线一般并不重合。

       编辑推荐：

       2024年中考各科目重点知识汇总

　　 欢迎使用手机、平板等移动设备访问中考网，2025中考一路陪伴同行！>>点击查看