来源:网络资源 2023-06-23 18:57:34
1、直角三角形中各元素间的关系
在△ABC中,C=90°,AB=c,AC=b,BC=a。
(1)三边之间的关系: a² +b²=c²。(勾股定理)
(2)锐角之间的关系:A+B=90°
(3)边角之间的关系:(锐角三角函数定义)
sinA=cosB=a/c, cosA= sinB=b/c,tanA=a/b。
2、斜三角形中各元素间的关系
在△ABC中,A、B、C为其内角,a、b、c分别表示A、B、C的对边。
(1)三角形内角和:A+B+C=π 。
(2)正弦定理:在一个三角形中,各边和它所对角的正弦的比相等。
形式一:a/sinA=b/sinB=c/sinC=2R(R为外接圆半径)
形式二:a=2RsinA,b=2RsinB,c=2RsinC(边化正弦)
形式三:a:b:c=sinA:sinB:sinC(比的性质)
形式四:sinA=a/2R,sinB=b/2R,sinC=c/2R(正弦化边)
(3)余弦定理:三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。
形式一:a²= b²+ c²- 2bccosA;
b²=c²+a² - 2cacosB;
c²=a²+b²- 2abcosC。
形式二:cosA=(b²+ c²-a²)/2bc,
cosB=(a²+ c²-b²)/2ac,
cosC=(a²+b²-c²)/2ab。
3、三角形的面积公式:
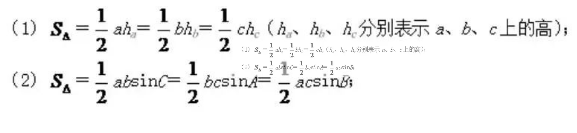
4、解三角形:
由三角形的六个元素(即三条边和三个内角)中的三个元素(其中至少有一个是边)求其他未知元素的问题叫做解三角形。广义地,这里所说的元素还可以包括三角形的高、中线、角平分线以及内切圆半径、外接圆半径、面积等等。主要类型:
(1)两类正弦定理解三角形的问题。
第 1、已知两角和任意一边,求其他的两边及一角。
第2、已知两角和其中一边的对角,求其他边角。
(2)两类余弦定理解三角形的问题:
第1、已知三边求三角。
第2、已知两边和他们的夹角,求第三边和其他两角。
5、三角形中的三角变换
三角形中的三角变换,除了应用上述公式和上述变换方法外,还要注意三角形自身的特点。
(1)角的变换
因为在△ABC中,A+B+C=π,所以sin( A+B )=sinC; cos(A+B)=-cosC;tan( A+B )=-tanC。

(2)判定三角形形状时,可利用正余弦定理实现边角转化,统一成边的形式或角的形式。
6、三角形的五心:
垂心一一三角形的三边上的高相交于一点
重心一一三角形三条中线的相交于一点
外心一一三角形三边垂直平分线相交于一点
内心一一三角形三内角的平分线相交于一点
旁心一一三角形的一条内角平分线与其他两个角的外角平分线交于一点
7、三角形诱导公式:
公式一:设α为任意角,终边相同的角的同一三角函数的值相等。
sin(2kπ+α)=sinα (k∈Z)
cos(2kπ+α)=cosα (k∈Z)
tan(2kπ+α)=tanα (k∈Z)
cot(2kπ+α)=cotα(k∈Z)
公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系。
sin(π+α)= -sinα
cos(π+α)=-cosα
tan(π+α)= tanα
cot(π+α)=cotα
公式三:任意角α与-α的三角函数值之间的关系(利用 原函数 奇偶性)。
sin(-α)=-sinα
cos(-α)= cosα
tan(-α)=-tanα
cot(-α)=-cotα
公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系。
sin(π-α)= sinα
cos(π-α)=-cosα
tan(π-α)=-tanα
cot(π-α)=-cotα
公式五利:用公式一和公式三可以得到2π-α与α的三角函数值之间的关系。
sin(2π-α)=-sinα
cos(2π-α)= cosα
tan(2π-α)=-tanα
cot(2π-α)=-cotα
公式六:π/2±α与α的三角函数值之间的关系。
sin(π/2+α)=cosα
sin(π/2-α)=cosα
cos(π/2+α)=-sinα
cos(π/2-α)=sinα
tan(π/2+α)=-cotα
tan(π/2-α)=cotα
cot(π/2+α)=-tanα
cot(π/2-α)=tanα
8、求解三角形应用题的一般步骤:
(1)分析:分析题意,弄清已知和所求;
(2)建模:将实际问题转化为数学问题,写出已知与所求,并画出示意图;
(3)求解:正确运用正、余定理求解;
(4)检验:检验上述所求是否符合实际意义。
编辑推荐:

欢迎使用手机、平板等移动设备访问中考网,2025中考一路陪伴同行!>>点击查看